24 Bit bei 96 khz. Der alltägliche Wahnsinn (Beta)

Überall werden 24/96 Soundkarten angeboten und jeder sagt sich „ah ja, hab mal gehört, daß die Soundkarte das unterstützen sollte“. Zu allem Überfluss gibt es darüber hinaus auch noch von einigen Herstellen 24 / 192 Soundkarten im Angebot.

Aber was bedeutet das denn nun eigentlich dieses 24/96?

Um dies zu erklären, muss ich vorher ein paar grundlegende Dinge erklären:

Bit-Depth

Die erste Zahl steht für die Bit-Depth, die auch Bitrate genannt wird. Sozusagen wie viele Lautstärke Abstufungen denn nun möglich sind. Es wird also zu jeder Lautstärke ein Wert zugeordnet. Die Genauigkeit der Klangverarbeitung hängt also unter anderem von der Bit-Depth ab.
Doch nun einmal gucken, wie viele Lautstärke-Abstufungen der Krempel ergibt:

Bei 1 Bit hat man entweder 0 oder 1 (also An oder Aus). Man hat also 2 Abstufungen.
Bei 2 Bit hat man dann 00, 01, 10, und 11. Das sind dann schon mal 4 Abstufungen.
Bei 3 Bit hat man 000, 001, 010, 011, 100, 101, 110, 111. Ergibt dann 8 Abstufungen.
Bei 4 Bit habe ich keine Lust mehr alles hinzuschreiben. Dann das sind dann schon 16 Abstufungen.
Bei 5 Bit werden es dann schon 32 Abstufungen.

Der ein oder andere wird bei der Betrachtung dieser Entwicklung der Zustandsmöglichkeiten schon dahinterkommen, wo das denn nun hinführt.
Es ist zu sehen, dass die Anzahl der Zustände ziemlich schnell zunimmt. Berechnen kann man die Anzahl mit der einfachen Formel 2 hoch n = Anzahl der Abstufungen (Lautstärke Abstufungen).

Noch mal die Werte für die wichtigsten Bitrates:

8 Bit: 256 Abstufungen
16 Bit: 65.536 Abstufungen
24 Bit: 16.777.216 Abstufungen
32 Bit: 4.294.967.296 Abstufungen

Sample-Rate

Die zweite Zahl in dem Gebilde 24/96 bezeichnet die Sample rate. Diese gibt Aufschluss über die Abtastrate. Aha, und was ist das?
Das bedeutet, wie oft der Computer (oder was auch immer) das Audio Signal pro Sekunde abtastet.

Da eine Schallwelle immer eine positive und auch eine negative Auslenkung hat, benötigt man die doppelte Abtastfrequenz. Höähhh?

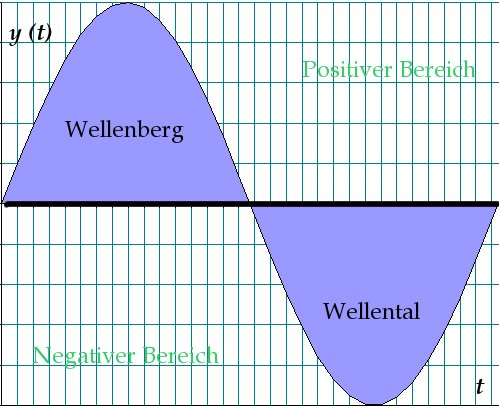
Sehen wir uns dazu mal folgende Grafik an:

Zu sehen ist hier ein einziger Sinuston. Natürlich ist diese optimiert, um nur einen Eindruck von Schall zu vermitteln.  Ein Ton besteht immer (!!!) aus einem Wellenberg und einem Wellental. Nun  könnte man einen Computer programmieren nur einen Wellenberg zu erzeugen, jedoch würde der Lautsprecher diesen Wellenberg in Wellenberg und Wellental umwandeln (wegen seiner Trägheit –> ein kurzer Impuls verursacht eine physikalische Schwingung).

Zurück zum Thema: Es sind mindestens 2 Messungen erforderlich, um zu ermitteln, dass es sich tatsächlich um ein Wellenberg und ein Wellental handelt. Das Ganze nennt man Nyquist-Abtasttheorem (eine sehr schöne Verdeutlichung von diesem ist bei den Links weiter unten zu finden). Ich versuche das ganze mal  zu verbildlichen:

Stellt euch ein Pendel vor. Das Pendel schwingt 2 mal pro Sekunde. Also „links—rechts—links—-recht“ und das innerhalb einer Sekunde. Nun habt ihr eine ganz tolle Handy-Video-Kamera, die aber voll langsam ist (also eher von 2010). Ihr könnt also gerade 2 Bilder (im gleichen Abstand) innerhalb einer Sekunde filmen. Was wird wohl zu sehen sein???  Antwort:  das Pendel bewegt sich gar nicht. Es ist 2 mal an der gleichen Stelle, da die Kamera zu lahm ist, um auch zu registrieren, dass das Pendel auch mal zwischendurch auf der anderen Seite ist. Ihr benötigt also eine Kamera die 4 Bilder in einer Sekunde registriert, damit ihr erahnen könnt, daß das Pendel sich auch echt bewegt. Genau so ist es mit dem Ton auch, bloß dass man nicht „sieht“, dass die Schallwelle hin und her „pendeln“.

Das menschliche Ohr nimmt Frequenzen zwischen ca. 20 und 20000 Hz wahr, wobei die Obergrenze mit zunehmenden Alter abnimmt. Also würde theoretisch (denkt man jetzt erst mal) eine Sample-Rate von ca. 40000 Hz reichen (also hörbaren 20000 Hz). Allerdings muss man noch ein paar Hertz abziehen, damit man auch den obersten Frequenzbereich noch verzerrungsfrei wahrnehmen kann.

Die Audio-CD hat eine Sample rate von 44100 Hz. Also schon mal gar nicht so schlecht, so ziemlich genau 20500 Hz (wegen der oben erwähnten Hälfte) können abgebildet werden.

Aber reicht das denn nicht aus? Nun ja…. einige Leute hören gerade in dem oberen Frequenzbereich viele Feinheiten (nicht unbedingt Otto-Normal-Verbraucher) raus, womit die Samplerate von 44100 Hz nicht ganz ausreicht. Man führte daraus resultierend die Sample rate 48000 Hz ein, die zur Zeit immer noch  bei vielen Filmproduktionen der Standard ist und auf diversen Audio-DVDs genutzt wird.  Bei dieser Samplerate kann man also also theoretisch 4000 Hz mehr hören (wieder wegen der Hälfte), als gehört werden kann.
Nahe der Grenzfrequenz kann es zu bösen Verzerrungen kommen, denen meistens (oder hoffentlich) mit einem Anti-Aliasing-Filter entgegengewirkt werden kann.
Dieser führt dazu, dass der obere Frequenzbereich dann etwas abgesenkt wird. Wenn man nun also aus den vollen Schöpfen will (also das Frequenzspektrum der menschlichen Ohren entsprechend) reicht eine Sample-Rate von 48000khz vollkommen aus. Dazu gibt es ganz viele Studien, wo Personen verschiedene Hörbeispiele in diversen Sample-Rates zu hören bekommen und entscheiden sollen, was denn nun besser klingt. Bei 48000khz war eigentlich Ende.

Doch wozu braucht man denn nun eine  Sample rate von 960000 Hz ?

Bei vielen komplexen Rechenvorgängen innerhalb des Computer werden feinste Feinheiten berechnet und noch mal verwurstet und dann noch mal verbogen. Besonders aufwändige Prozesse finden beispielsweise bei der Hallberechnung statt, da dort mit einer hohen Signaldichte gearbeitet wird. Da das menschliche Ohr aus Erfahrung sehr wohl weiß, wie ein Hall klingt, lässt es sich halt nicht so schnell verarschen und kann sehr gut zuordnen, wenn irgendetwas nicht stimmt.

Deswegen werden bei vielen digitalen Hall-Prozessoren Sample rates verwendet, die praktisch nicht hörbar sind, allerdings im Resultat doch einen Unterschied machen.  Diese Berechnungen laufen intern im Rechner ab. Selbst wenn das Signal vorher mit 8 Bit bei einer Samplerate von 22000 Hz in solch ein Gerät geschoben wird, arbeitet das Gerät intern z.B: mit 192000 Hz Samplerate. Der einzige Haken an der Sache ist, dass das Ausgangssignal wieder runter gerechnet wird auf 48khz bzw. auf  44.1khz bei einer handelsüblichen Audio CD. Eigentlich ist also dieser Bereich bei der Aufnahme eher den Fledermäusen unter euch zugunsten entstanden. Ok es gibt noch Impulstreue und tralala..für mich aber nichts weiter als eine Mischung aus planlosigkeit und pseudo-Elitärem Geschwafel.

Noch mal zurück zur Bit-Depth. Wir erinnern uns an die 65.536 Abstufungen (oder auch diskrete Werte) die sich bei 16 Bit ergeben. Leider gibt es ja noch die Sache mit den Wellenberg und dem Wellental. In den 65.536 Abstufungen sind also negative und positive Werte enthalten. Da Schalldrücke aber sowohl positive wie auch negative Auslenkungen einer Welle beinhalten, ergeben sich somit 32.768 sinnvolle Abstufungen (da die Welle ja digital übertragen werden muss). Schade ist daran nur, dass alle Werte, die nicht so recht in diese Skale fallen, einfach falsch zugeordnet werden. Den Kram nennt man dann Quantisierungsfehler, den man von der Dynamik abziehen muss. Diese fallen dann in die Kategorie Rundungsfehler, sind aber bei solch feinen Abstufungen irgendwie verkraftbar und für den Normalverbraucher eh nicht hörbar.

Noch Ein paar Fakten:

Mit 1 Bit läßt sich ungefähr ein Dynamikumfang von 6 db abbilden.  Der Grund dafür liegt in einer ätzenden mathematischen Umformung mit Logarithmen und Wurzeln und so, aber das will ich nun wirklich keinem zumuten!

Bei 16 Bit kommt man also auf 96dB Dynamikumfang und bei 24 Bit auf einen Dynamikumfang von 144 db.

Die empfundene Lautheit wird bei einem Zuwachs von 10dB verdoppelt.

Die Schmerzschwelle liegt zwischen 120dB und 130dB.

Und wie viel ist nun sinnvoll?

Tja, da gibt es so eine Einheit, die die Lautstärke beschreibt und sich Phon nennt. Ab 3 Phon hört ein Mensch etwas und ab 130 Phon tut es schon weh. Unterschiede von 1 Phon sind nicht hörbar. Daraus ergibt sich dann—> 128 Schritte, wenn man komplette Stille dazu nimmt, wenn der Verstärker so laut aufgedreht ist, dass es bei dem 127. Schritt schon weh tut. Hmm, wozu braucht man denn nun 16.777.216 Abstufungen bei 24 Bit? Wer die Antwort weiß, kann dies gerne ausführlich kommentieren. Fairerweise sollte man dazu noch sagen, dass die Signale ja noch nachbearbeitet werden und verbogen und gekrümmt, aber da sollten eigentlich die 32.766 Abstufungen locker reichen. Fairerweise muss ich hier natürlich noch den Headroom einführen der beim recording eine essentielle Rolle spielt. Ich verkürze das mal etwas….beim recording ergeben 24 Bit aufnahmen Sinn. Man kann halt viel flexibler mit zu leisen Signalen umgehen, aber beim Mixdown (bzw. bei der fertigen CD) kann auch ruhig schon mal der Tatsache ins Auge geblickt werden, dass der Verstärker halt nicht mehr lauter werden kann bzw. dass man nicht einen Düsenjet im Wohnzimmer haben möchte.

Da war doch noch was..ach ja. Was ist eigentlich, wenn die Abtastung nicht immer konstant ist? Das würde nun wirklich den Rahmen sprengen, aber soviel mal vorweg:  Das nennt man Jitter und passt eigentlich auch gar nicht so recht hier rein. Stell dir einfach vor ,dein billig Handy von 2008 macht mal 2 und dann 3 Bilder pro Sekunde beim Filmdreh. Das Ergebniss wird unschön; das ist Jitter!

Ein Grundlegendes Problem bei der ganzen Geschichte ist meiner Ansicht nach, dass niemand zu Hause einen Verstärker so weit aufreißen würde (oder so einen besitzt), dass er so laut ist wie ein startendes Flugzeug (um wirklich alle feinen Nuancen der Dynamik zu hören) und auch fast niemand so gute Ohren hat den Kram auch noch zu registrieren. Dazu kommen dann noch die bescheidenen Abhörmöglichkeiten, von Stereoortung ganz zu schweigen. Es ist utopisch zu verlangen, dass ein Musikhörer die optimalen Abhörbedingungen hat. Trotz allem sollte man natürlich bemüht sein, die optimalen Grundvoraussetzungen als Mischer zu ermöglichen, aber irgendwo ist halt auch mal Ende der Fahnenstange.

Noch zu erwähnen:

Ein Vorteil der sich aus der Erhöhung der Sample Rate ergibt ist die Verringerung der Latenz beim HD-Recording. Diese kann man meiner Ansicht nach aber auch genauso gut auf anderen Wegen gegen null streben lassen und ist somit eigentlich irrelevant.

Es gibt einen Spezialfall beim dem hohe Samplerates beim recording (und nur hier) Sinn ergeben und zwar, wenn man vor hat später das Signal extrem runter pitchen möchte und damit die unhörbaren Frequenzen in den hörbaren Bereich verschiebt. Jedoch benötigt man hierfür ein Mikrofon, dass diese Frequenzen aufnehmen kann und da wird es dann schon Dünne.

Die Erhöhung der Bitrate wie auch die Erhöhung der Sample-Rate verursacht bei gleicher Spieldauer eine Audio-Datei eine höhere Datenmenge mit der der Computer klar kommen muss und auch die Festplattenkapazität sollte bei enorm krassen Einstellungen nicht unterschätzt werden.

Selbst zusammengebasteltes Glossar:

Bitrate

Als Bitrate bezeichnet man das Verhältnis von einer Datenmenge zur Zeit, also im Prinzip die Bit depth und die Sample rate zusammen, innerhalb eines definierten Zeitraums.

dB:

db steht für Dezibel und ist eine relative, einheitslose Größe. Bei Null dB ist die sogenannte Hörschwelle definiert. Es gibt auch ein absoluten Pegel, jedoch wurde hier erst ein Norm wert eingeführt, auf dem sich das Ganze bezieht, also eigentlich eine Mogelpackung.

http://de.wikipedia.org/wiki/Dezibel#Definition_von_Bel_und_Dezibel

Quellen und Weiterführende Links:

http://de.wikipedia.org/wiki/Audioformat

http://de.wikipedia.org/wiki/Phon_(Akustik)

http://www.sengpielaudio.com/RechnerSonephon.htm

Eine sehr schöne Verdeutlichung zum Abtasttheorem (ab Seite 3)

http://www.preuss-media.de/datenreduktion/index.html

http://de.wikipedia.org/wiki/Jitter

http://de.wikipedia.org/wiki/Quantisierungsfehler

http://old.hfm-detmold.de/eti/projekte/diplomarbeiten/1998/seite1.html

http://www.analog.com/en/content/0,2886,760%255F%255F88014,00.html

http://de.wikipedia.org/wiki/Schmerzschwelle

Nachtrag:

Dieser Beitrag wurde von mir lange lange vorbereitet und ist eigentlich immer noch im Betastadium und wird sicherlich noch aktualisiert, da ich immer wieder weitere Ideen verarbeite die ich einfließen lassen werde, aber irgendwann muss der Kram ja mal raus.